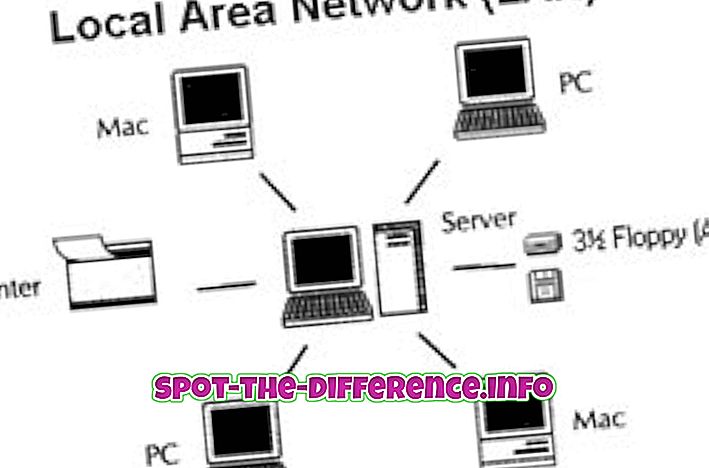
Nøgleforskel: En parabola er en konisk sektion, der skabes, når et plan skærer en konisk overflade parallelt med konusens side. En hyperbola skabes, når et plan skærer en konisk overflade parallelt med aksen.

Parabola og hyperbola er to forskellige ord, sektioner og ligninger, der anvendes i matematik til at beskrive to forskellige sektioner af en kegle. Disse er forskellige i form, størrelse og forskellige andre faktorer i formler, der bruges til at beregne det. For at forstå dem, lad os først forstå keglen og de forskellige koniske sektioner.

Et konisk afsnit er en kurve, der opnås, når et plan skærer med en kegle på forskellige måder. De nedskæringer, der opnås fra skæringen, omfatter ellipse, cirkel, parabola og hyperbola. Ifølge analytisk geometri defineres konisk som "en plan algebraisk kurve i grad 2." Den populære definition af konisk sektion omfatter et fokuspunkt, directrix linje og excentricitet. Fokuspunktet og direktelinjelinjerne forventes at være i en fast ration i en konisk. Forholdet er kendt som ekscentriciteten af ​​den koniske sektion. Excentriciteten af ​​ellipser, paraboler og hyperboler adskiller sig; ellipser har en ekscentricitet mindre end 1, parabolas har en ekscentricitet, der er lig med 1, og hyperboler har en ekscentricitet større end 1. Det tidligste kendte arbejde på koniske sektioner kan dateres tilbage til det fjerde århundrede f.Kr. af Menaechmus, der opdagede en måde at løse problemet med at fordoble terningen gennem brug af parabolaer.

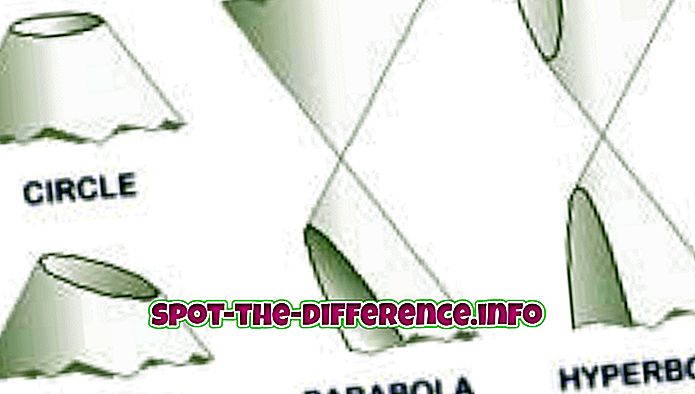
En parabola er en konisk sektion, der skabes, når et plan skærer med en kegle. Parabolaer eller paraboler danner 'fra skæringspunktet mellem en ret cirkulær konisk overflade og et plan parallelt med en genererende retlinie af overfladen.' En anden måde, som en parabola er skabt, er, når et punktpunkt på et fly, der er lige langt fra fokuset og direktoren, skaber en parabola. I algebra anvendes paraboler ofte i grafer af kvadratiske funktioner ved hjælp af formlen y = x ^ 2.

En linje, der deler parabolen gennem midten, kaldes symmetriaksen; denne linje er også vinkelret på direktoren og passerer gennem fokus. De punkter, der er på symmetriaksen, der skærer parabolen, kaldes 'vertex'. Afstanden mellem vertex og fokus er kendt som "brændvidde". Paraboler kan åbne i begge retninger inklusive op, ned, højre eller venstre. Også et hovedtræk ved paraboler er, at de er alle de samme, kun forskellige i størrelse. De kan omplaceres og omskalkes nøjagtigt til at passe til enhver anden parabola. Paraboler anvendes i forskellige anvendelser såsom billygter reflektorer, design af ballistiske missiler mv. De spiller også en stor rolle i fysik, teknik, matematik mv.

Hyperboler er en glat kurve, der opstår, når et plan skærer med keglen parallelt med y-aksen, der skaber et snit langs keglens side. En hyperbola er defineret af dens geometriske egenskaber eller ligninger, for hvilke det er et opløsningssæt. Udtrykket "hyperbola" er afledt af det græske ord, som betyder "overkastet" eller "overdreven". Udtrykket er antaget at være dannet af Apollonius af Perga, som har bidraget meget til studiet af koniske sektioner.

En hyperbola er kendt for at have grene, der er spejlbilleder til hinanden og ligner to uendelige buer. Punkterne på de to grene, som er tættest på hinanden, kaldes krydsene. Linjen, der forbinder vertikalerne, er kendt som tværgående akse eller hovedakse, hvilket svarer til hoveddiameteren af ​​en ellipse. Midterpunktet på en tværgående akse er kendt som hyperbolas centrum. Ligningen af ​​en hyperbola er skrevet som x2 / a2-y2 / b2 = 1. Hyperboler anvendes i forskellige applikationer i nutidens verden, herunder stien efterfulgt af skyggen af ​​spidsen af ​​en sol, form af et åbent kredsløb; Den bruges som en bue i mange konstruerede bygninger, som ligninger i matematik og geometri, fysik mv.

Hyperboler og paraboler er begge åbne kurver, hvilket betyder, at de ikke slutter og fortsætter på ubestemt tid til uendelig, noget som ellipser og cirkler ikke kan gøre.