Hovedforskel: I computere er de binære træer datadata strukturer, der lagrer dataene, og giver brugeren adgang til, søge, indsætte og slette dataene i algoritmisk tid. Forskellen mellem et B og B + -træ er, at i et B-træ kan tasterne og dataene gemmes i både de interne og blade noder, hvorimod i et B + træ kun dataene og nøglerne kan lagres i bladnoderne .

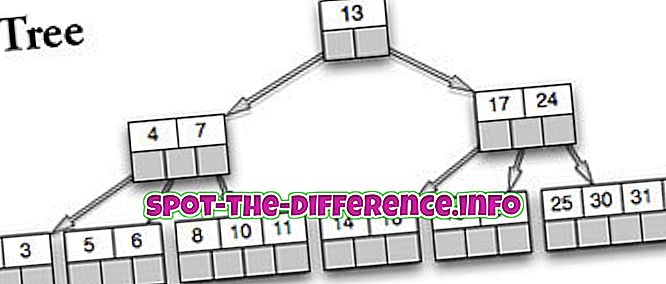
De binære træer er afbalancerede søgetræer, der er designet til at fungere godt på sekundære lagringsenheder med direkte adgang som f.eks. Magnetiske diske. Rudolf Bayer og Ed McCreight opfandt begrebet et B-træ.

Et B-træ er et generaliseret binært søgetræ, hvor enhver knude kan have mere end to børn. Hver intern knude i et B-træ indeholder et antal nøgler. Disse nøgler adskiller værdierne og danner endvidere undertræerne. De interne knudepunkter i et B-træ kan have varierende antal børne noder, som er arrangeret inden for et foruddefineret område. På det tidspunkt, hvor data er indsat eller fjernet fra en hvilken som helst knude, er der en ændring i antallet af børne noder. For at opretholde det foruddefinerede område kan interne knuder være forbundet eller splittet. I et B-træ er der tilladt en række børne noder, hvorfor det foruddefinerede område skal opretholdes.

B-træerne behøver ikke at blive genbalanceret ofte i modsætning til andre selvbalancerende søgetræer. Knuderne i disse træer er ikke altid fulde; Derfor bliver rummene forbrugt unødvendige i disse træer, der fører til spild af plads. Kun de nederste og øvre grænser på antallet af børne noder er typisk fastgjort til en bestemt implementering. For eksempel i et 2-3 B-træ (ofte simpelthen omtalt som et 2-3 træ), kan hver intern knude kun have 2 eller 3 barn noder.

Derudover er B-træet optimeret til systemer, der læser og skriver store databaser. Det bruges almindeligvis i databaser og filsystemer. I B-træet holdes alle knuder på samme balancedybder fra rodknudepunkterne. Disse dybder stiger langsomt, idet antallet af elementer stiger; dette resulterer i, at alle bladnoder er en mere knude længere væk fra roden. Desuden er B-træerne mere fordelagtige sammenlignet med andre implementeringer i forhold til den tid, der tages for at få adgang til dataene.

Et B + -træ er et n-array-træ med en node, som består af et stort antal børn pr. Knude. Roten kan være et blad eller en knude, der indeholder mere end to børn. Et B + træ består af en rod, interne knuder og blade.

Et B + træ er det samme som et B-træ; Den eneste forskel er, at i B + træet er der et ekstra niveau tilføjet nederst med linkede blade. I modsætning til B-træet indeholder hver knude i et B + også kun nøgler og ikke nøgleværdipar.

Derudover måler balanceringsfaktoren eller rækkefølgen af ​​et B + træ kapacitet for de interne knudepunkter i et træ, dvs. antallet af knuder, de kan have. Det egentlige antal børn til en node er begrænset til interne noder. Roten er dog en undtagelse, da det er tilladt at have mere end to antal børn. For eksempel, hvis rækkefølgen af ​​et B + -træ er 7, kan hvert internt knudepunkt (bortset fra roden) have mellem 4 og 7 børn; mens roden kan have mellem 2 og 7. Den primære værdi af B + træet er at lagre data for effektiv hentning i en blokorienteret opbevaringskontekst og især filsystemer.

Den primære værdi af B + træet er i lagring og vedligeholdelse af dataene, således at dataene ikke går tabt. Denne fremgangsmåde anvendes især i blokorienteret opbevaringskontekst og i nogle bestemte filsystemer. Bladene, som er de nederste indeksblokke af B + -træet, er ofte forbundet med hinanden i en tilknyttet liste; Derfor gør det rækkevidde forespørgsler eller en ordnet iteration gennem blokkene enklere og mere effektiv. Yderligere er rumfaktoren ikke spildt i B + træer. B + træet giver et effektivt boligdata strukturformat, hvilket gør dem enkle at få adgang til og lagre. B + træerne er særligt nyttige som et databasesystemindeks, hvor dataene typisk ligger på en disk.

Sammenligning mellem B Tree og B + Tree: